Wie Viel Grad Hat Ein Dreieck Insgesamt

In diesen Erklärungen erfährst du, welche Dreiecke es gibt, welche Eigenschaften sie haben und welche speziellen Linien im Dreieck existieren. Weiter erfährst du, wie du den Umfang und den Flächeninhalt eines Dreiecks berechnen kannst.

Allgemeines Dreieck und seine Winkelsumme

Jedes Dreieck chapeau drei Eckpunkte, drei Seiten und drei Winkel.Für dice Beschriftung der Eckpunkte eines Dreiecks verwendest du große Buchstaben in alphabetischer Reihenfolge (zum Beispiel A, B und C). Die Beschriftung erfolgt üblicherweise gegen den Uhrzeigersinn.Die Seiten werden mit kleinen Buchstaben (zum Beispiel a, b und c) beschriftet. Dabei liegt die Seite a dem Eckpunkt A gegenüber und verbindet dice Punkte B und C. Nach dem gleichen Prinzip werden die beiden anderen Seiten beschriftet.Für Winkel werden kleine griechische Buchstaben verwendet (zum Beispiel α, β und γ). Dabei ist α der Winkel am Eckpunkt A, β liegt am Eckpunkt B und γ am Eckpunkt C.Die Summe der Innenwinkel eines Dreiecks beträgt

$180°$

.

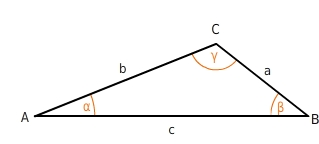
Winkelsumme: α + β + γ =

$180°$

Winkelsumme im Dreieck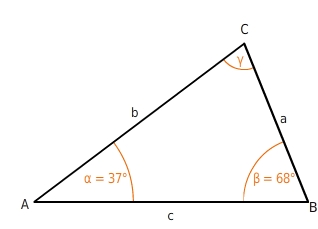

Dreiecksarten und ihre Eigenschaften

Es gibt verschiedene Dreiecksarten. Du kannst diese nach der Größe ihrer Winkel und nach der Länge ihrer Seiten einteilen:Winkelgröße: Seitenlänge: Winkelgröße und Seitenlänge lassen sich auch kombinieren, wobei die Seitenlänge immer zuerst genannt wird (zum Beispiel „gleichschenklig-rechtwinkliges Dreieck").

Spitzwinkliges DreieckIn einem spitzwinkligen Dreieck sind alle Winkel kleiner als

$90°$

.

Rechtwinkliges DreieckIn einem rechtwinkligen Dreieck ist ein Winkel genau

$90°$

groß.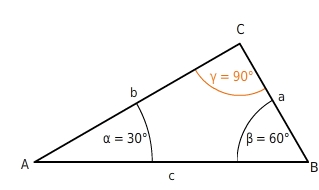

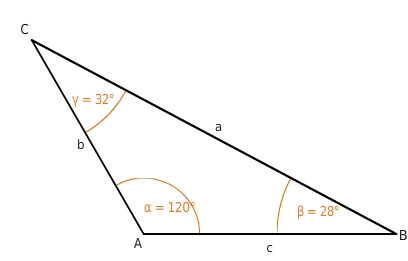
Stumpfwinkliges DreieckIn einem stumpfwinkligen Dreieck ist ein Winkel größer als

$90°$

.

Gleichschenkliges DreieckIn einem gleichschenkligen Dreieck sind zwei Seiten (die beiden Schenkel) gleich lang. Der Schnittpunkt der beiden Seiten heißt Spitze. Die dritte Seite wird Basis genannt, und die beiden an der Ground anliegenden Winkel sind die Basiswinkel.

Spezielle gleichschenklige Dreiecke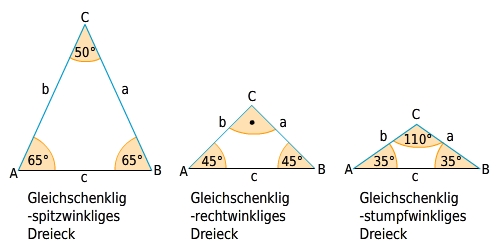

Gleichseitiges DreieckIn einem gleichseitigen Dreieck sind alle Seiten gleich lang und alle Winkel gleichgroß (

$60°$

).

Achsensymmetrie bei Dreiecken

Eine Figur, dice an einer Geraden g auf sich selbst gespiegelt werden kann, heißt achsensymmetrisch zur Geraden m. Diese Gerade heißt Symmetrieachse.

Gleichschenkliges Dreieck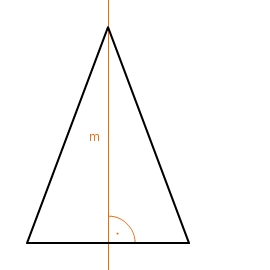

Gleichseitiges Dreieck

Spezielle Linien im Dreieck

Im Dreieck gibt es spezielle Linien, auch Transversalen genannt, die den Eckpunkten oder Seiten des Dreiecks zugeordnet sind:- Höhe- Mittelsenkrechte- Seitenhalbierende- WinkelhalbierendeJede Höhe eines Dreiecks ist eine Strecke, geht durch einen Eckpunkt und steht senkrecht auf der gegenüberliegenden Dreiecksseite oder deren Verlängerung.Höhen sind wichtig für die Berechnung des Flächeninhalts eines Dreiecks.

Jede Mittelsenkrechte eines Dreiecks ist eine Gerade und verläuft senkrecht durch den Mittelpunkt einer der Dreiecksseiten.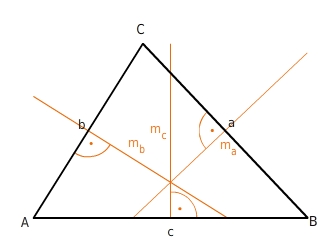

Jede Seitenhalbierende eines Dreiecks ist eine Strecke und verbindet einen Eckpunkt des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite.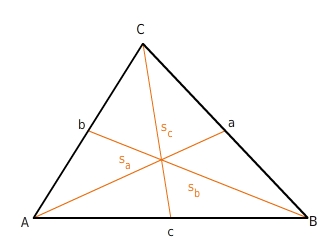

Jede Winkelhalbierende eines Dreiecks ist eine Halbgerade und teilt den dazugehörigen Winkel in zwei gleich große Winkel.

Höhen in einem stumpfwinkligen Dreieck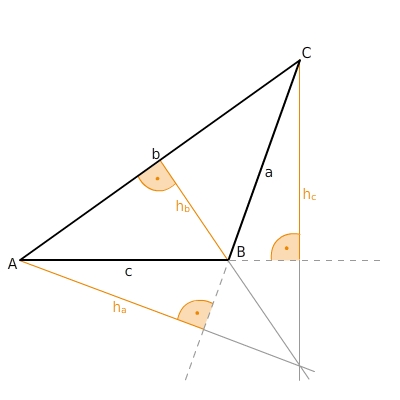

Mittelsenkrechten in einem stumpfwinkligen Dreieck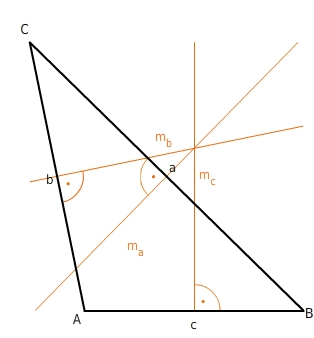

Spezielle Linien im gleichseitigen Dreieck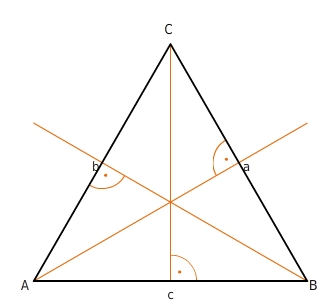

Umfang und Flächeninhalt eines Dreiecks

Den Umfang U eines Dreiecks berechnest du, indem du alle Seitenlängen addierst. Werden die Seitenlängen eines Dreiecks mit a, b und c bezeichnet, dann berechnest du den Umfang mit folgender Formel:

$\text{U}=\text{a}+\text{b}+\text{c}$

Den Flächeninhalt eines Dreiecks (A) berechnest du, indem du dice Länge der Grundseite yard mit der zugehörigen Höhe h multiplizierst und das Produkt durch 2 dividierst:

$\text{A}=\frac{\mathrm{one}}{2}\text{g}·\text{h}$

Da es drei verschiedene Grundseiten und die jeweiligen zugehörigen Höhen im Dreieck gibt, gibt es drei verschiedene Möglichkeiten den Flächeninhalt zu berechnen:

$\text{A}=\frac{1}{2}\text{a}·{\text{h}}_{\text{a}}$

, wobei a die Länge einer Seite und

${\text{h}}_{\text{a}}$

die zugehörige Höhe bezeichnet.

$\text{A}=\frac{\mathrm{one}}{2}\text{b}·{\text{h}}_{\text{b}}$

, wobei b dice Länge einer Seite und

${\text{h}}_{\text{b}}$

die zugehörige Höhe bezeichnet.

$\text{A}=\frac{1}{2}\text{c}·{\text{h}}_{\text{c}}$

, wobei c dice Länge einer Seite und

${\text{h}}_{\text{c}}$

die zugehörige Höhe bezeichnet.Den Flächeninhalt eines rechtwinkligen Dreiecks (A) berechnest du, indem du die Längen der Seiten, die den rechten Winkel einschließen, multiplizierst:

$\text{A}=\frac{1}{2}\text{a}·\text{b}$

, wobei a und b dice Längen der Seiten, die den rechten Winkel einschließen, bezeichnen.

Umfang eines Dreiecks:

$\text{U}=\text{a}+\text{b}+\text{c}$

Flächeninhalt eines Dreiecks:

$\text{A}=\frac{1}{2}\text{a}·{\text{h}}_{\text{a}}=\frac{\mathrm{i}}{2}\text{b}·{\text{h}}_{\text{b}}=\frac{\mathrm{i}}{\mathrm{ii}}\text{c}·{\text{h}}_{\text{c}}$

Flächeninhalt eines rechtwinkligen Dreieck:

$\text{A}=\frac{\mathrm{ane}}{2}\text{a}·\text{b}$

Woher kommt die Formel zur Flächeninhaltsberechnung eines Dreiecks? 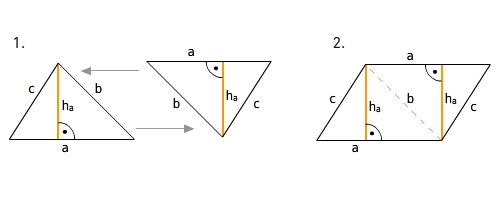Wenn du zwei identische Dreiecke wie im Bild anlegst, erhältst du ein Parallelogramm. Daher ist der Flächeninhalt eines Dreiecks gleich der Hälfte des Flächeninhalts des erhaltenen Parallelogramms.Woher kommt die Formel zur Flächeninhaltsberechnung eines rechtwinkligen Dreiecks? 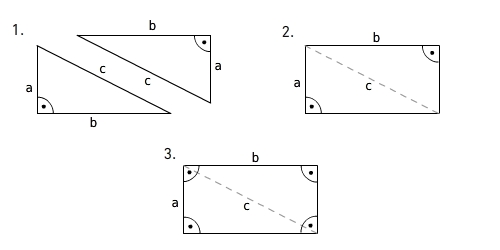Wenn du zwei deckungsgleiche rechtwinklige Dreiecke wie im Bild anlegst, erhältst du ein Rechteck mit Länge a und Breite b. Daher ist der Flächeninhalt eines rechtwinkligen Dreiecks gleich der Hälfte des Flächeninhalts des Rechtecks.

Flächeninhalt eines DreiecksBerechne den Flächeninhalt des Dreiecks.

Flächeninhalt berechnen

$\text{A}=3026{\text{cm}}^{\mathrm{ii}}$

Flächeninhalt eines rechtwinkligen DreiecksBerechne den Flächeninhalt des Dreiecks.

Flächeninhalt berechnen

$\text{A}=403{\text{cm}}^2$

Berechnung einer Seitenlänge im DreieckVon einem Dreieck sind der Umfang U =

$\mathrm{nineteen}\mathrm{cm}$

und zwei Seitenlängen a =

$6\mathrm{cm}$

und b =

$3\mathrm{cm}$

gegeben. Berechne dice Länge der dritten Seite c.

Seitenlänge berechnen

Berechnung einer Höhe im DreieckVon einem Dreieck sind der Flächeninhalt A =

$42{\mathrm{1000}}^2$

und die Seitenlänge a =

$12\mathrm{yard}$

gegeben. Berechne die zugehörige Höhe.

Höhe berechnen

${\text{h}}_{\text{a}}=7\text{thousand}$

Dreiecksungleichung

Die Dreiecksungleichung besagt:In jedem Dreieck ist eine Seitenlänge immer kleiner als die Summe der beiden anderen Seitenlängen.Mit Hilfe der Dreiecksungleichung kannst du überprüfen, ob ein Dreieck konstruierbar ist. Umgekehrt golden, dass jedes Dreieck die Dreiecksungleichung erfüllt.

Beispiel für ein konstruierbares Dreieck Mit den Seitenlängen a =

$\mathrm{iv.five}\mathrm{cm}$

, b =

$\mathrm{vi}\mathrm{cm}$

und c =

$7.5\mathrm{cm}$

ist ein Dreieck konstruierbar.

Beispiel für ein nicht konstruierbares DreieckMit den Seitenlängen a =

$3\mathrm{cm}$

, b =

$5\mathrm{cm}$

und c =

$\mathrm{ten}\mathrm{cm}$

ist kein Dreieck konstruierbar.

Source: https://de.bettermarks.com/mathe/eigenschaften-von-dreiecken/

Share this post